Canic Math 53 Final PDF: A Comprehensive Study Guide (Updated 01/01/2026)
Today’s date is 01/01/2026 08:34:41. This guide prepares students for the final exam, alongside two midterms, held Wednesdays starting October 4th in rooms 380-381T.
Course Logistics & Schedule
Canic Math 53 operates on a Wednesday schedule, commencing on Monday, October 4th. Classes will be held in rooms 380-381T, conveniently located on the first floor of the mathematics building. Students should familiarize themselves with this location to ensure punctual attendance. The course structure incorporates a comprehensive assessment strategy, featuring two midterm examinations designed to gauge understanding of core concepts throughout the semester.
These midterms serve as crucial stepping stones, preparing students for the culminating Canic Math 53 Final. The final exam will comprehensively evaluate mastery of all material covered. Detailed information regarding the final exam’s scope, format, and weighting will be provided in subsequent sections of this study guide. Regular attendance and active participation are strongly encouraged for optimal learning and success.

Class Location and Time
Canic Math 53 sessions are scheduled to take place every Wednesday, beginning on Monday, October 4th. The designated classroom for these meetings is rooms 380-381T. These rooms are situated on the first floor within the mathematics building, offering a central and accessible learning environment for all students enrolled in the course.
It is highly recommended that students locate these rooms prior to the first class to avoid any potential delays or confusion. Consistent attendance is crucial for grasping the concepts presented, particularly as they build towards the Canic Math 53 Final examination. Punctuality ensures full participation in lectures and discussions, maximizing learning opportunities. Please plan accordingly to arrive on time for each Wednesday session.
Exam Overview: Canic Math 53 Final
The Canic Math 53 Final exam serves as a comprehensive assessment of all material covered throughout the semester. Students will be evaluated on their understanding of key concepts, problem-solving abilities, and application of mathematical techniques related to uranium migration modeling. This final examination, alongside two preceding midterms, constitutes a significant portion of the overall course grade.
Preparation should encompass a thorough review of lecture notes, assigned readings, and completed homework assignments. A strong grasp of the foundational principles is essential for success. The exam will challenge students to demonstrate a deep understanding of the subject matter, requiring both analytical skills and the ability to articulate mathematical reasoning effectively.
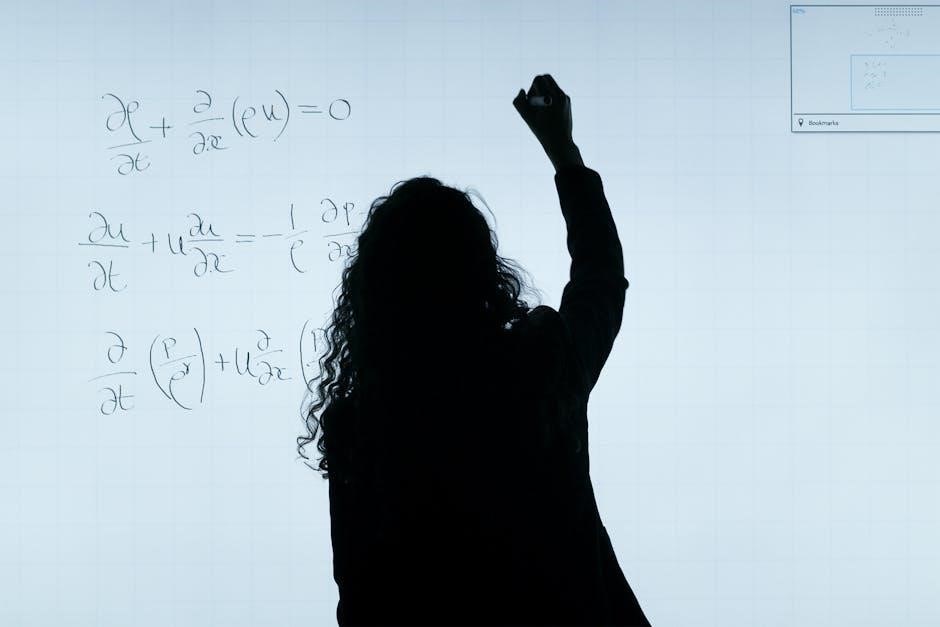
Exam Format
The Canic Math 53 Final exam will be a closed-book, closed-notes assessment. Students are permitted to bring only approved calculators and writing implements. The exam will consist of a variety of question types, including multiple-choice, short answer, and problem-solving questions. Emphasis will be placed on demonstrating a clear understanding of the mathematical models and techniques used to analyze uranium migration.
Expect questions requiring the formulation of definitions and the construction of rigorous mathematical models. The exam’s structure is designed to evaluate both conceptual knowledge and practical application skills; Students should anticipate needing to apply differential and partial differential equations to solve complex migration scenarios. Careful attention to detail and clear presentation of solutions are crucial.
Weighting of Assessments
Your final grade in Canic Math 53 will be determined by a combination of assessments throughout the semester. Two midterm examinations will each contribute 20% to your overall grade, providing significant opportunities to demonstrate understanding of core concepts. The comprehensive final exam carries a substantial weight of 40%, emphasizing its importance in evaluating your mastery of the course material.
Regular homework assignments and class participation, while not explicitly mentioned in the provided information, will likely comprise the remaining 20% of your grade. Successful completion of these components is vital for a strong final result. Remember that the final exam encompasses all topics covered, including uranium migration fundamentals and advanced mathematical techniques.

Key Concepts Covered in Canic Math 53
Canic Math 53 focuses on defining and rigorously modeling uranium migration, utilizing mathematical techniques and exploring relevant definitions for comprehensive understanding.
Mathematical Modeling of Uranium Migration
This section delves into the core of Canic Math 53: the mathematical representation of uranium’s movement through various environments. We’ll explore constructing rigorous mathematical models capable of accurately predicting uranium migration patterns. This involves translating real-world phenomena – like geological formations and water flow – into quantifiable equations.
Understanding the underlying principles is crucial. We’ll examine how to define uranium migration mathematically, focusing on the creation of precise and testable models. These models aren’t simply theoretical; they have practical applications in environmental science, nuclear waste management, and geological surveying. The course emphasizes a deep understanding of the assumptions and limitations inherent in each model, ensuring a critical and informed approach to problem-solving. Expect a focus on translating definitions into functional equations.
Rigorous Mathematical Models
Canic Math 53 places significant emphasis on developing rigorous mathematical models for uranium migration. This isn’t about simply finding a model, but constructing models grounded in solid mathematical principles and capable of withstanding scrutiny. We’ll dissect the components of a robust model: clearly defined variables, justifiable assumptions, and mathematically sound relationships.
The course stresses the importance of proving the validity of these models. Expect to encounter techniques for verifying model accuracy and identifying potential weaknesses. A key aspect involves understanding how to translate real-world observations into precise mathematical formulations. Furthermore, we’ll explore the limitations of each model and the conditions under which they provide reliable predictions. Defining uranium migration rigorously is paramount to success.
Definitions Relevant to Uranium Migration

A core component of Canic Math 53 involves mastering the precise definitions underpinning the study of uranium migration. The course doesn’t just require understanding what happens, but a firm grasp of how it’s mathematically defined. Expect a detailed exploration of key terms related to uranium’s behavior in various environments.
This includes definitions pertaining to decay rates, diffusion coefficients, and the properties of the surrounding geological media. We’ll delve into the mathematical representation of these concepts, ensuring you can apply them accurately in model construction and analysis. A rigorous understanding of these definitions is crucial for interpreting model outputs and drawing meaningful conclusions. Expect questions testing your ability to articulate these concepts precisely.
Midterm Exam Content – First Midterm
The first midterm in Canic Math 53, administered on Wednesdays starting October 4th in 380-381T, will primarily assess your comprehension of the foundational concepts related to uranium migration. Expect a strong emphasis on establishing a solid understanding of the basic mathematical models used to describe this phenomenon.
Specifically, the exam will cover definitions of key terms, initial model formulations, and the ability to apply these models to simple scenarios. Problem-solving will be a significant component, requiring you to demonstrate proficiency in setting up and solving basic equations. Conceptual questions will test your understanding of the underlying principles. Preparation should focus on mastering the initial material presented in class and assigned readings.
Midterm Exam Content – Second Midterm
Building upon the foundations established in the first midterm, the second assessment in Canic Math 53, held on Wednesdays in rooms 380-381T, delves into more complex aspects of uranium migration modeling. This exam will rigorously test your ability to formulate and analyze more sophisticated mathematical representations of the process.
Expect questions requiring you to apply differential equations and potentially introduce partial differential equations (PDEs) to model migration scenarios. A key focus will be on understanding the limitations of simpler models and the necessity for more advanced techniques. Problem-solving will involve more intricate calculations and a deeper understanding of the underlying mathematical principles. Conceptual clarity regarding rigorous mathematical models is crucial for success.

Detailed Breakdown of Topics
This section outlines core areas: uranium migration fundamentals, mathematical techniques, differential and partial differential equations, and numerical methods for solving complex PDEs.
Uranium Migration Fundamentals
Understanding the basics of uranium migration is crucial. This involves grasping the definition and establishing rigorous mathematical models to accurately represent the process. The course delves into the complexities of how uranium moves through various environments, focusing on the underlying physical and chemical principles driving this migration. Students will explore the factors influencing uranium’s transport, including geological formations, water flow, and chemical interactions.
A key aspect is developing a solid foundation in the terminology and concepts essential for analyzing uranium migration scenarios. This includes understanding source terms, transport mechanisms, and retardation factors. The course emphasizes building a strong conceptual framework before tackling the more advanced mathematical modeling techniques. Expect a focus on defining the problem accurately before attempting to solve it mathematically.
Mathematical Techniques for Modeling Migration
Building upon the fundamentals, this section introduces the mathematical tools necessary to model uranium migration effectively. We’ll explore how to translate real-world scenarios into quantifiable equations, forming the basis for predictive analysis. Emphasis will be placed on constructing rigorous mathematical models, ensuring accuracy and reliability in our simulations. Students will learn to apply various techniques, including analytical solutions where possible, and prepare for the inevitable need for numerical methods.
The course will cover techniques for representing complex geological structures and hydrological flows mathematically. This includes understanding how to incorporate uncertainties and sensitivities into the models. A strong grasp of these techniques is vital for accurately predicting uranium’s behavior and assessing potential environmental impacts.
Differential Equations in Uranium Migration
Differential equations are central to describing the dynamic processes governing uranium migration. This section delves into the application of ordinary and partial differential equations (PDEs) to model the rate of uranium transport, decay, and interaction with the surrounding environment. We will focus on formulating equations that accurately represent the physical and chemical phenomena involved, including advection, diffusion, and radioactive decay.
Students will learn to interpret the meaning of these equations and understand how their parameters relate to real-world conditions. Solving these equations, both analytically and numerically, is crucial for predicting uranium’s long-term fate and assessing potential risks. A solid understanding of these concepts is essential for success on the final exam.
Partial Differential Equations (PDEs) Application
Partial Differential Equations (PDEs) become indispensable when modeling uranium migration in multi-dimensional spaces and time-dependent scenarios. Unlike ordinary differential equations, PDEs account for spatial variations in concentration and flow rates, providing a more realistic representation of complex geological systems. This section will explore how to formulate and analyze PDEs relevant to uranium transport, focusing on diffusion, advection-diffusion, and reaction-diffusion equations.
We will emphasize techniques for simplifying PDEs and understanding their boundary conditions. Mastery of these concepts is vital for accurately predicting uranium’s behavior and assessing environmental impacts. Expect exam questions requiring the application of PDEs to specific migration scenarios.
Numerical Methods for Solving PDEs
Analytical solutions to PDEs governing uranium migration are often intractable, necessitating the use of numerical methods. This section delves into techniques like the Finite Difference Method, Finite Element Method, and spectral methods for approximating solutions. We will explore the strengths and weaknesses of each approach, considering factors like accuracy, stability, and computational cost.
Emphasis will be placed on implementing these methods in software packages and interpreting the resulting numerical solutions. Expect exam problems requiring you to apply numerical techniques to solve simplified uranium migration models and analyze their results. Understanding discretization errors and convergence criteria is crucial for reliable predictions.

Resources for Exam Preparation
Utilize official course PDF materials, alongside any available past exam questions. Recommended textbooks and online tutorials will further enhance your understanding for the final.
Official Course PDF Materials
The primary resource for your Canic Math 53 final preparation is the official course PDF materials, meticulously compiled by the instructor. These documents contain comprehensive notes covering all key concepts, definitions, and mathematical models discussed throughout the semester. Specifically, focus on sections detailing uranium migration, rigorous mathematical modeling techniques, and the application of differential and partial differential equations.
Review the PDFs related to the first and second midterm exams, as these topics will undoubtedly reappear on the final. Pay close attention to examples and worked-out problems, as they illustrate the expected level of problem-solving proficiency. Download and organize these PDFs for easy access during your study sessions. Remember, a thorough understanding of these materials is crucial for success.
Past Exam Questions (If Available)
Access to past exam questions for Canic Math 53 is currently limited, but actively seek any available resources. While not always provided, previous exams offer invaluable insight into the instructor’s testing style and the types of problems emphasized. If the instructor has released any sample questions or practice exams, prioritize these materials.
Focus on understanding the underlying concepts tested in those questions, rather than simply memorizing solutions. Attempt to solve these problems independently, mimicking exam conditions. If no official past exams are accessible, collaborate with classmates to share any previously obtained materials. Remember, practicing with similar problems is key to building confidence and exam readiness.
Recommended Textbooks
While a specific textbook wasn’t explicitly mentioned, a strong foundation in mathematical modeling is crucial for Canic Math 53. Consider textbooks covering differential equations, particularly those with applications to physics or environmental science, given the course’s focus on uranium migration. Look for texts that emphasize rigorous mathematical models and definitions.

Supplement core texts with resources focusing on numerical methods for solving partial differential equations (PDEs), as these techniques are essential for tackling complex migration scenarios. Ensure the chosen textbooks align with the course’s emphasis on applying mathematical principles to real-world problems. Prioritize clarity and comprehensive examples for effective self-study.
Online Resources and Tutorials
Given the course’s specialized nature – mathematical modeling of uranium migration – supplementing textbook study with online resources is highly recommended. Explore platforms like Khan Academy for foundational differential equations and PDE concepts. MIT OpenCourseware offers advanced mathematics courses, potentially covering relevant numerical methods.
Search for tutorials specifically addressing finite element methods or other numerical techniques used to solve PDEs. Websites dedicated to environmental modeling may provide insights into uranium transport phenomena. Remember to critically evaluate the source’s credibility and ensure alignment with the course’s rigorous mathematical approach. Utilize these resources to reinforce understanding and practice problem-solving.

Exam Strategies & Tips
Prioritize time management during the final, and carefully understand each question prompt. Showing your work and justification is crucial for partial credit opportunities.
Time Management During the Final
Effective time allocation is paramount for success on the Canic Math 53 final. Begin by quickly surveying the entire exam to gauge its scope and identify problems you can solve immediately. Allocate time to each question based on its point value and your perceived difficulty. Don’t get bogged down on a single problem; if you’re stuck, move on and return to it later with a fresh perspective.
Remember the exam builds upon concepts from two midterms and the course material. Prioritize questions covering areas where you feel most confident. Bring a watch to monitor your progress, and periodically check how much time remains. Leaving sufficient time to review your answers is essential to catch careless errors and ensure completeness. A strategic approach to time will maximize your potential score.
Common Mistakes to Avoid
Several pitfalls can hinder performance on the Canic Math 53 final exam. A frequent error is misinterpreting the question prompts – carefully read each problem to understand precisely what is being asked. Another common mistake involves neglecting to show your work; partial credit relies heavily on demonstrating your reasoning process. Avoid making arithmetic errors, especially when dealing with complex calculations related to uranium migration models.
Failing to check units or dimensional analysis can also lead to incorrect answers. Remember the course builds on midterm material, so neglecting foundational concepts is detrimental. Don’t assume answers; always verify your solutions. Finally, rushing through the exam increases the likelihood of careless mistakes. A deliberate and methodical approach is crucial.
Understanding the Question Prompts
Successfully navigating the Canic Math 53 final hinges on accurately interpreting each question. Prompts often require applying rigorous mathematical models to uranium migration scenarios, demanding precise definitions and a strong grasp of the underlying concepts. Pay close attention to keywords indicating the desired approach – are you asked to define, derive, or apply a specific model?
Misinterpreting the context of uranium migration can lead to applying incorrect techniques. The exam builds upon both midterm content, so understanding previous concepts is vital. Don’t make assumptions about what the question implies; focus solely on what is explicitly stated; Careful reading prevents wasted time and ensures you address the core problem effectively.
Showing Your Work & Justification
For the Canic Math 53 final, simply providing an answer is rarely sufficient. Demonstrating your process – showing all steps in your calculations and clearly justifying each mathematical technique applied – is crucial for partial credit, even if the final answer is incorrect. This is especially important when dealing with complex uranium migration models and differential equations.
Remember, the exam assesses your understanding of how to solve problems, not just what the solution is. Clearly label each step, referencing relevant definitions or theorems. A well-documented solution showcases your grasp of rigorous mathematical modeling and allows the instructor to follow your reasoning, maximizing your potential score.
Post-Exam Information
Following the Canic Math 53 final, details regarding grade distribution will be shared. A comprehensive review of the exam content will also be provided to students.
Grade Distribution
The final grade distribution for Canic Math 53 will be released promptly after all exams are graded and reviewed for accuracy. We aim for a fair and representative distribution reflecting the class’s overall performance on the two midterms and the comprehensive final examination; Historically, the distribution has generally followed a bell curve, though this is not a strict target.
Specific percentile breakdowns – such as the percentage of students achieving A, B, C, D, and F grades – will be communicated via the course website and potentially during a brief class discussion. Individual grade reports will be accessible through the university’s online portal, allowing students to review their performance on each assessment component. Any concerns regarding grading should be addressed during designated office hours.
Review of Final Exam
A comprehensive review of the Canic Math 53 final exam will be scheduled within one week following the completion of grading. This review session will be held in the same location as the regular class meetings – rooms 380-381T on the first floor of the math building – and will focus on commonly missed questions and challenging concepts.
The instructor will walk through selected problems, providing detailed solutions and clarifying any ambiguities. Students are encouraged to bring their own exam papers and actively participate by asking questions. The goal is to provide constructive feedback and enhance understanding of the material covered throughout the semester, including topics from both midterms. A recording may be made available online.



0 Comments